Throughout college, I’ve felt like February can be one tough month. Maybe it’s because classes have restarted at school, activities are back in action, and I still haven’t recovered enough sleep from the Fall semester. Or it could be that I went an entire two weeks of college without a laptop (which surprisingly made me a lot more productive). Maybe it’s due to the fact that it’s cold outside, and that the low for today in Baltimore is -4 degrees F (and earlier this week my building’s heat shut off on the chilliest day since 1905…really…and its going to be shut off again tonight). Or maybe it’s because one of my best friends is spending time in Sydney, Australia for the semester, where it’s currently in the 80’s.

On the bright side though…it’s the last full month of winter. Days are getting longer and Spring is right around the corner. My junior year second semester is almost a third of the way over (WAT) and I can tell it’s already going to fly by. Now…I’m not going to spend this post on big picture questions like I did previously…this time I’ve got a specific problem for you. And…it involves how close you are to bacon.

^^ Not that bacon (though it does look lovely right now…and also heart attack inducing…so still lovely). We’re actually going to look at how close you are to Bacon, well, Kevin Bacon to be exact.

Any 21st century student who has a mild addiction to social media (so everyone), has heard the simple question…”how many degrees of separation am I from Kevin Bacon?” In reality, this is a play on the classic “six degrees of separation” concept that states that there are 6 or fewer “steps” to between every person in the world. The concept, first publicized by Hungarian author Frigyes Karinthy, can be seen in his short story “Chain Links“. Kevin Bacon became involved when actors/actresses/film industry staff members in Hollywood began to trace their connections to Kevin Bacon through mutual acquaintances. The number of people between themselves and Kevin Bacon eventually became known as their “Bacon Number”

Now…how do we find our own Bacon Number or, more generally, the separation between us and another person? Now, we’re going to use a little help from… GRAPH THEORY (anticlimax ensues). No…we’re not looking at the y=mx+b graphs you probably fretted over in math class.

These graphs are a little different. Imagine you have a set of dots on a piece of paper, which we’ll call “vertices”. Each dot represents a person in the world. Then, we’ll draw a line, or “edge” between two vertices if the people representing those vertices know each other. Therefore, we have a graph representing simple social connections between people. To illustrate a simple example, I drew up a little graph of my family. There are vertices for my mom, myself, my brother, my grandmother and my great-grandmother. My mom, brother, grandmother and I know each other, but only my mom and grandmother met my great-grandmother. Therefore, there are edges between those who know each other, and no edges between people who have never met. Check it out here:
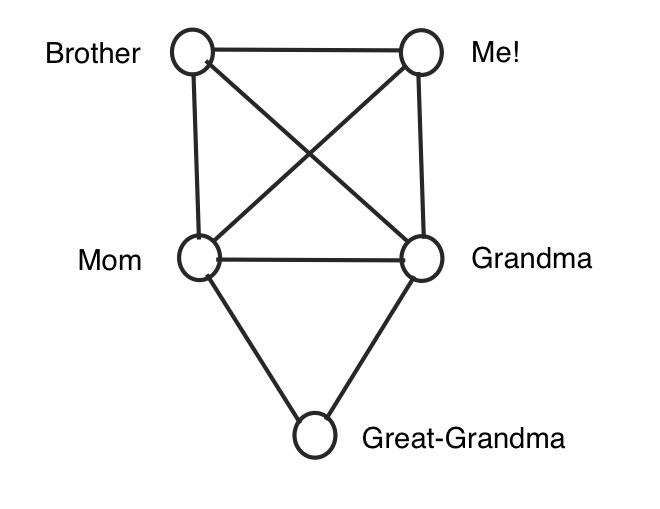
Now…in this graph, pick any vertex and leave it through one of the edges connected to it. Continue doing this until you stop at any vertex. Crossing edges between vertices is called “traversing” a vertex, and doing this along edges continuously creates a “walk” in the graph. A walk without any repeated vertices is called a “path” and the “length” of a path is the amount of edges traversed between two vertices.
So…sorry for all of the terminology, but now let’s go back to our original problem. With this graph-model in our pocket, how can we see the degrees of separation between us and another person? Well…it’s simply the length of the shortest path between two vertices. For example, my mom and I only have one degree of separation, since there is only a single edge between us. On the other hand, my great-grandmother and I have two degrees of separation, because the length of the shortest path between us (which is either me to my mother and then to my great-grandmother, or me to my grandmother and then my great-grandmother) is two. Get it?

So you try…talk to people you’re close with and see if you can find links to others throughout the world. By computing this graph model you might be able to easily find your own Bacon Number (mine’s only 3)!
Now…if you think this is a little trivial…graph theory can do a bit more work to trace the social connections between people and show some pretty neat ideas. For instance, take a look at your Facebook “Suggested Friends” list. How do you think Facebook finds out which people to play here? What Facebook does is actually draw out a graph connecting you to each person you’re friends with, and then draws another edge from your friends to people they are friends that you currently do not know. Note that these are each paths of length 2. It then computes how many of these paths lead to the same person, and uses this number as the likelihood that you will know that person Pretty sick right! This is all the basis of social networking theory…and Facebook graphs can get pretty intense:
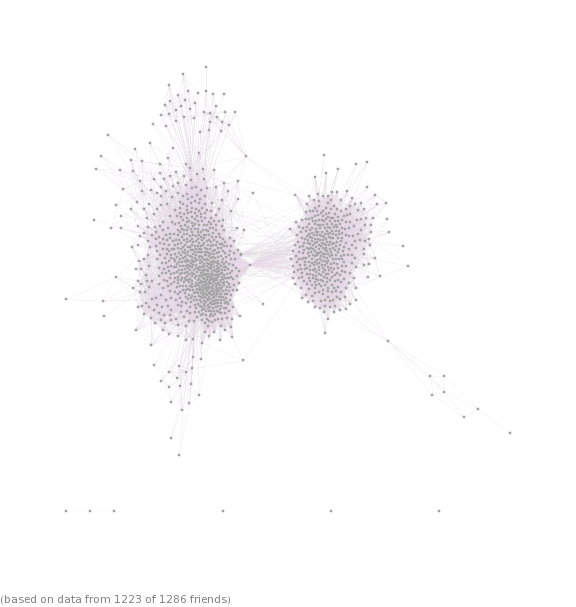
So that’s a wrap. If you stuck with me, I hope you found that detour into Applied Math pretty cool! Just realize how awesome it is to live in a world where we can be so connected to such a large body of people. As a college junior…you realize how much your small social network impacts you, and this tiny network is comprised of your closest friends. Personally, I don’t think I would have been able to get through another tough February without them. And there’s a lot of beauty in that.
-Dadler 🙂

