This is a blog about two things. One is the field of engineering, which is seen as a rigorous discipline combining the two wonderfully interesting (depending upon your personality) fields of math and science. The other, is the beautiful. But just to spark your interest as to why I might be writing about engineering and the beautiful we can play a little game. Let’s look at two images. The first below:

and the second…
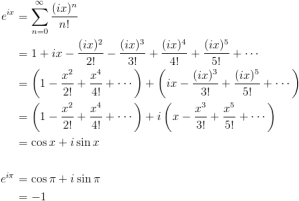
Now…raise your right hand if you thought the word beauty sits with the first image better than the second, and your left if you think the opposite. I could guess where about 95% + of you would fall into place. The first image is obviously a collections of Dickens book, written by one of the greatest authors of all time, and the second, if you didn’t know…is a case of Euler’s Identity. Now we all know the beauty in Dickens (some of you might not be the biggest fan of his long descriptions though), but what makes the second image beautiful? Is it really possible to call Euler’s Identity a beautiful work?
Euler’s identity relates what is considered to be the five most important numbers in mathematics, thus being e, i, pi, 1 and 0 if you think of the formula e^(i*pi) + 1 = 0. It also relates some of the most important functions we use on a daily basis, including the exponential (e), sine (sin) and cosine (cos).
Now some of you might not be convinced yet that relating all of these things could be considered beauty…but I’ll try to add some more insight. Without these functions we wouldn’t know anything about this:
nor would we be able to describe this:

or you wouldn’t be able to make more of these quite as fast:

…and let’s be honest, the solar system, a day at the beach, and some dolla dolla bills (y’all) are beautiful things. Euler’s Identity relates numbers and functions that can model the rotation of our planets, help show the oscillations and cycle of tides, and show how we can accumulate compound interest when we make a bank deposit. Though the numbers on the page may not be beautiful themselves, the implications of Euler’s Identity produces beauty…and it’s pure simplicity almost makes it beautiful in itself.
So you might not be convinced, and maybe you’ll never be. But, if you stick with me a little bit, maybe I can help find an engineering topic of interest that you might find some beauty in as well.
-Dadler

